Introduction to Bigraphical Models for Algebraic Swarm Equations
Wait—equations for swarms?
Yes—algebraic equations, but with a twist: they come with visual notations built from (bi)graphical structures.
This matters when working with systems like drone swarms or robot collectives—where agents move in space, interact locally, and must coordinate globally. Algebra here isn’t just numbers; it’s a language for structure. Combined with visual bigraphs, it becomes a powerful tool for describing collective behaviors.
Algebraic Spaces
Bigraphs extend ordinary graphs with two complementary dimensions:
- Locality – who is “inside” or “near” whom
- Connectivity – who is linked or able to communicate
By combining these, bigraphs provide a unified algebraic and visual framework for systems where geometry meets interaction.
We extend bigraphs into so-called bi-spatial structures — modular, grid-like building blocks that define discrete spatial layouts.
These can model drones flying in formation, robots sorting themselves on a grid, or agents exploring an environment.
Examples
The following figures illustrate exemplary topological structures built from this “syntax of space” (which are formalized using our bigraphical axioms):
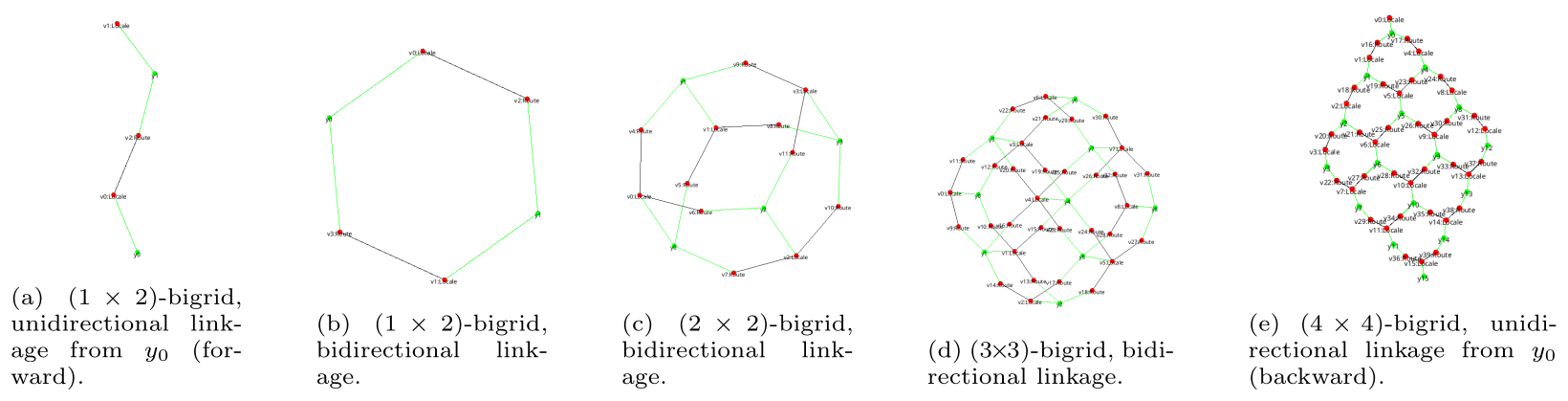
Why It Matters
- Concrete + formal: Models are both visually intuitive and mathematically precise.
- Composable: Complex swarms are built from simple axioms (“bi-spatial axioms”), ensuring modularity.
- Dynamic: Agents evolve via reaction rules, giving rise to algebraic swarm equations that capture both motion and coordination.
- Debuggable: Equations can be analyzed by calculators and through extensions like 3D raycasting, swarm evolution can be observed in real time.
Foundations of UniAgent: Bigraphical Models
The UniAgent platform builds on a small set of bi-spatial axioms—algebraic rules that define how discrete locales connect. These axioms form the backbone for modeling swarms as algebraic spaces, where agents move and interact.
Think of them as the Lego-bricks of swarm modeling: simple, composable, and grounded in both algebra and geometry.
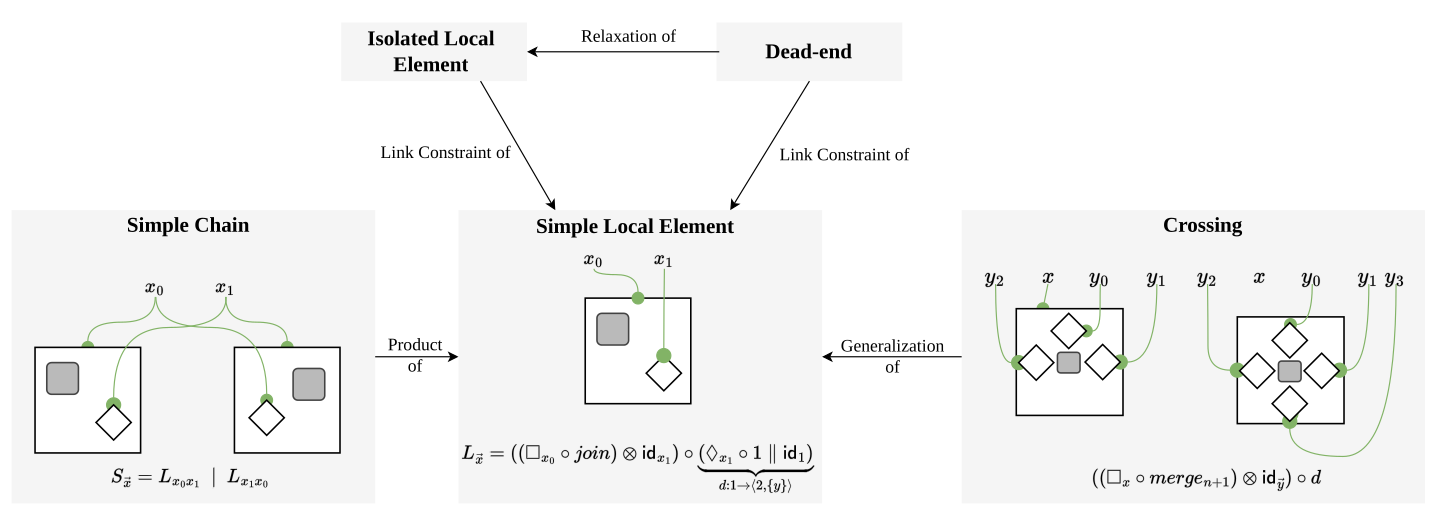This figures presents an overview of the bi-spatial axioms.
Read more about it here: